الاعداد الحقيقية والعمليات عليها

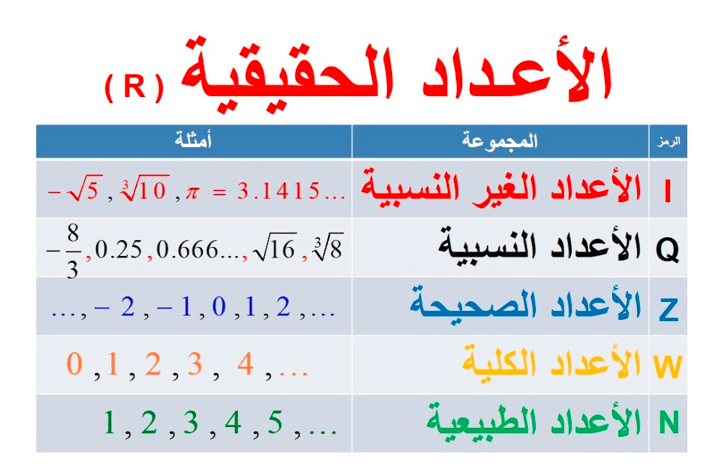
الاعداد الحقيقية هي مجموعة لا نهائية من الأرقام التي يمكن تصورها على خط مستقيم. وهي تشمل الأعداد النسبية والغير نسبية، والموجبة والسالبة، وحتى الصفر. وفي السطور التالية نوضح كافة التفاصيل على موقع بسيط دوت كوم.

الاعداد الحقيقية

تعرف الأعداد الحقيقية بأنها الأعداد التي يمكن تمثيلها على خط الأعداد، وقد يكون العدد الحقيقي صحيح أو كسري، موجب أو سالب، فالمهم أن يكون مربّعها حقيقيًا موجبًا.

أنواع الأعداد الحقيقية

تنقسم الأعداد الحقيقية إلى قسمين رئيسيين:

1. الأعداد النسبية: وهي الأعداد التي يمكن كتابتها ككسر، مثل 3/2 أو 1.5.
2. ثم الأعداد غير النسبية: وهي الأعداد التي لا يمكن كتابتها ككسر، مثل الجذر التربيعي لـ2 أو العدد π.

ترتيب الأعداد الحقيقية

يمكن ترتيب الأعداد الحقيقية على خط الأعداد من اليسار إلى اليمين، بحيث تكون الأعداد السالبة على اليسار، والأعداد الموجبة على اليمين، والصفر في المنتصف.

عمليات الأعداد الحقيقية

يمكن إجراء العمليات الحسابية الأساسية على الأعداد الحقيقية، مثل الجمع والطرح والضرب والقسمة.

أمثلة على الأعداد الحقيقية

فيما يلي بعض الأمثلة على الأعداد الحقيقية:

• الأعداد الطبيعية: 1، 2، 3، …
• الأعداد الصحيحة: …، -3، -2، -1، 0، 1، 2، 3، …
• ثم الأعداد الكسرية: 1/2، 3/4، 5/6، …
• الأعداد غير النسبية: الجذر التربيعي لـ2، العدد π، …

أهمية الاعداد الحقيقية

تستخدم الأعداد الحقيقية في العديد من المجالات العلمية والرياضية، مثل الهندسة والجبر والرياضيات المالية. كما أنها تستخدم في الحياة اليومية، مثل حساب المسافات والكميات والأسعار.

بعض التطبيقات العملية للأعداد الحقيقية

• استخدام الأعداد الحقيقية لحساب المسافات والكميات في الهندسة والجبر.
• استخدام الأعداد الحقيقية لحساب الفوائد والأسعار في الرياضيات المالية.
• ثم استخدام الأعداد الحقيقية لحساب درجات الحرارة والكميات في العلوم.
• ثم استخدام الأعداد الحقيقية لحساب السرعة والزمن في الفيزياء.

من اين تبدأ الاعداد الحقيقية؟

تبدأ الأعداد الحقيقية من الصفر، حيث يمثل الصفر نقطة التقاطع بين خط الأعداد الموجبة وخط الأعداد السالبة. وعلى خط الأعداد، تقع الأعداد الموجبة على يمين الصفر، وتقع الأعداد السالبة على يسار الصفر.

وبشكل أكثر تحديدًا، يمكن القول أن الأعداد الحقيقية تبدأ من الصفر، وتستمر إلى ما لا نهاية في كلا الاتجاهين، أي إلى الأعداد الموجبة وإلى الأعداد السالبة. وهذا يعني أن هناك عددًا لا نهائيًا من الأعداد الحقيقية، منها:

• الأعداد الصحيحة، مثل 1، 2، 3، 4، …
• ثم الأعداد الكسرية، مثل 1/2، 3/4، 1/3، …
• ثم الأعداد غير النسبية، مثل π، √2، e، …

وعلى الرغم من أن الأعداد الحقيقية تبدأ من الصفر، إلا أنه يمكننا أيضًا القول أنها تبدأ من أي عدد حقيقي آخر. فعندما نقول أن العدد 1 أكبر من العدد -1، فإننا نعني أن 1 يقع إلى يمين -1 على خط الأعداد.

وبنفس الطريقة، عندما نقول أن العدد π أكبر من العدد 3، فإننا نعني أن π يقع إلى يمين 3 على خط الأعداد. ولذلك، يمكننا القول أن الأعداد الحقيقية تبدأ من أي عدد حقيقي، وتستمر إلى ما لا نهاية في كلا الاتجاهين.

ما هو الفرق بين العدد الصحيح والعدد الحقيقي؟

الفرق بين العدد الصحيح والعدد الحقيقي هو أن العدد الصحيح هو عدد لا يحتوي على أجزاء كسريّة، بينما العدد الحقيقي هو أي عدد يمكن تمثيله على خط الأعداد، بما في ذلك الأعداد الصحيحة والكسور.

بشكل أكثر تحديدًا، يمكن تعريف العدد الصحيح على أنه عدد يمكن كتابته بدون استخدام الكسور أو الفواصل العشرية. ويشمل الأعداد الطبيعية (1، 2، 3، …) والصفر والأعداد السالبة المقابلة للأعداد الطبيعية (-1، -2، -3، …).

أما العدد الحقيقي فهو أي عدد يمكن تمثيله على خط الأعداد، بما في ذلك الأعداد الصحيحة والكسور. ويشمل الأعداد الصحيحة والكسور والأرقام غير النسبية، مثل √2 و π.

أمثلة على الأعداد الصحيحة

فيما يلي بعض الأمثلة على الأعداد الصحيحة:

• عدد المقاعد في الصف الواحد في الفصل الدراسي
• عدد الطلاب في المدرسة
• ثم عدد الأيام في الشهر
• ثم عدد الساعات في اليوم.

أمثلة على الأعداد الحقيقية

فيما يلي بعض الأمثلة على الأعداد الحقيقية:

• طول قطعة من الخشب
• وزن شخص
• ثم درجة الحرارة
• ثم الوقت.

جدير  الذكر يمكن القول أن العدد الصحيح هو مجموعة فرعية من مجموعة الأعداد الحقيقية. وتتميز الأعداد الصحيحة بأنها لا تحتوي على أجزاء كسريّة، بينما تشمل الأعداد الحقيقية الأعداد الصحيحة والكسور والأرقام غير النسبية.

هل الصفر ينتمي لمجموعة الاعداد الحقيقية؟

نعم، الصفر ينتمي لمجموعة الأعداد الحقيقية. مجموعة الأعداد الحقيقية هي مجموعة من جميع الأعداد التي يمكن العثور عليها على خط الأعداد، وهي تشمل الأعداد النسبية وغير النسبية، والموجبة والسالبة، وحتى الصفر. ثم يمكن تعريف الصفر بأنه عدد حقيقي ليس موجبًا وليس سالبًا. إنه نقطة التقاطع بين المحورين السالب والموجب على خط الأعداد.

يمكن أيضًا تعريف الصفر بأنه عدد حقيقي يكون مجموع أي عدد حقيقي معه هو نفس العدد الحقيقي. على سبيل المثال، 0 + 5 = 5. وبالتالي، فإن الصفر ينتمي لمجموعة الأعداد الحقيقية لأنه يلبي تعريفات مجموعة الأعداد الحقيقية.

هل الاعداد الحقيقية سالبة؟

نعم، يمكن أن تكون الأعداد الحقيقية سالبة. حيث أن الأعداد الحقيقية هي مجموعة من الأعداد التي يمكن تمثيلها على خط الأعداد، ويمكن أن تكون هذه الأعداد صحيحة أو كسورية، موجبة أو سالبة، فالمهم أن يكون مربّعها حقيقيًا موجبًا.

الأعداد السالبة هي أعداد حقيقية أصغر من الصفر، مثل -2، -5، -100، إلخ. يتم تمثيل الأعداد السالبة على خط الأعداد إلى يسار الصفر. إليك بعض الأمثلة على الأعداد الحقيقية السالبة:

• درجة الحرارة في الخارج هي -10 درجة مئوية.
• مديونية شخص ما هي 1000 دولار.
• ارتفاع شخص ما هو 165 سم.

لذلك، يمكننا القول أن الأعداد الحقيقية يمكن أن تكون سالبة، ويمكن استخدامها لتمثيل مجموعة متنوعة من القيم، مثل درجات الحرارة، والمبالغ المالية، والأبعاد.

تطبيقات الأعداد الحقيقية

تستخدم الأعداد الحقيقية في العديد من التطبيقات في الرياضيات والعلوم والهندسة، من أهمها:

• حساب المسافات والزوايا والكميات الأخرى في الهندسة.
• حل المعادلات والأنظمة الخطية وغير الخطية.
• دراسة الدوال والعلاقات الرياضية.
• تمثيل البيانات والقياسات.

أمثلة على الأعداد الحقيقية والغير حقيقية

فيما يلي بعض أمثلة على الأعداد الحقيقية والغير حقيقية:

• العدد 0
• ثم الأعداد الطبيعية
• ثم الأعداد الصحيحة
• الأعداد الكسرية
• الأعداد غير النسبية.

إن الأعداد الحقيقية هي مجموعة لا نهائية من الأرقام التي يمكن استخدامها لتمثيل أي كميّة مستمرة في العالم الحقيقي. تتمتع الأعداد الحقيقية بالعديد من الخصائص التي تجعلها أداة قوية للرياضيات والعلوم والهندسة.

كيف اعرف الاعداد الحقيقية؟

يمكن معرفة الأعداد الحقيقية من خلال تعريفها، حيث تُعرَّف الأعداد الحقيقية بأنها جميع الأعداد التي يمكن العثور عليها على خط الأعداد، وهي تشمل الأعداد النسبية وغير النسبية، والموجبة والسالبة، وحتى الصفر. فيما يلي بعض الخصائص التي تحدد الأعداد الحقيقية:

• يمكن تمثيل الأعداد الحقيقية على خط الأعداد.
• ثم يمكن إجراء العمليات الحسابية الأساسية على الأعداد الحقيقية، مثل الجمع والطرح والضرب والقسمة.
• ثم يمكن ترتيب الأعداد الحقيقية بشكل تصاعدي أو تنازلي.

أمثلة على الأعداد الحقيقية الصف الرابع

يمكن أيضًا معرفة الأعداد الحقيقية من خلال أمثلة منها، حيث تشمل الأعداد الحقيقية:

• الأعداد الطبيعية: 1، 2، 3، 4، …
• الأعداد الصحيحة: …، -3، -2، -1، 0، 1، 2، 3، …
• ثم الأعداد الكسرية: 1/2، 3/4، 5/6، …
• ثم الأعداد غير النسبية: √2، √3، √5، …

أمثلة على الأعداد الحقيقية الصف الخامس

فيما يلي بعض الأمثلة على الأعداد الحقيقية للصف الرابع والخامس:

• الارتفاع فوق مستوى سطح البحر: 100 متر، -100 متر، 0 متر.
• درجة الحرارة: 20 درجة مئوية، -20 درجة مئوية، 0 درجة مئوية.
• الوزن: 50 كيلوجرام، -50 كيلوجرام، 0 كيلوجرام.
• الوقت: 10:00 صباحًا، -10:00 صباحًا، 0:00 صباحًا. وبشكل عام، يمكن القول أن أي رقم يمكن تمثيله على خط الأعداد هو رقم حقيقي.

ما هي الاعداد الحقيقيه والغير حقيقيه؟

الأعداد الحقيقية هي مجموعة من الأرقام التي يمكن تمثيلها على خط الأعداد، وهي تشمل الأعداد النسبية والغير النسبية، والموجبة والسالبة، وحتى الصفر.

الأعداد غير الحقيقية هي مجموعة من الأرقام التي لا يمكن تمثيلها على خط الأعداد، وهي تشمل الأعداد التخيلية، مثل √-1 و 2 + 3i و -i.

تعريف الأعداد الحقيقية

الأعداد الحقيقية هي مجموعة من الأرقام التي تلبي الخصائص التالية:

• يمكن تمثيلها على خط الأعداد.
• ثم يمكن استخدامها في جميع العمليات الحسابية الأساسية، مثل الجمع والطرح والضرب والقسمة.
• ثم لها خصائص معينة، مثل خصائص التبديلية والجمع والتوزيعية.

أنواع الأعداد الحقيقية

الأعداد الحقيقية تنقسم إلى نوعين رئيسيين:

• الأعداد النسبية: هي الأعداد التي يمكن التعبير عنها ككسر، مثل 1/2 و 3/4 و 5/6.
• ثم الأعداد غير النسبية: هي الأعداد التي لا يمكن التعبير عنها ككسر، مثل √2 و √3 و √5.

تعريف الأعداد غير الحقيقية

الأعداد غير الحقيقية هي مجموعة من الأرقام التي لا يمكن تمثيلها على خط الأعداد، وهي تشمل الأعداد التخيلية.

الأعداد التخيلية

إن الأعداد التخيلية هي الأعداد التي تحتوي على وحدة تخيلية، وهي الحرف “i”. وتُعرف الأعداد التخيلية أيضًا بالأعداد العقدية.

خصائص الأعداد التخيلية

الأعداد التخيلية لها خصائص معينة نوضحها في صورة أمثلة على الأعداد الحقيقية، مثل:

• يمكن تمثيلها على خط الأعداد المركبة.
• ثم يمكن استخدامها في جميع العمليات الحسابية الأساسية، مثل الجمع والطرح والضرب والقسمة.
• ثم لها خصائص معينة، مثل خصائص التبديلية والجمع والتوزيعية.

استخدامات الأعداد الحقيقية والأعداد غير الحقيقية

تستخدم الأعداد الحقيقية في العديد من المجالات، مثل الرياضيات والفيزياء والهندسة. وتستخدم الأعداد التخيلية في مجال الهندسة الكهربائية والمعادلات التربيعية.

هل كل الاعداد اعداد حقيقية؟

لا، ليست كل الأعداد أعداد حقيقية. مجموعة الأعداد الحقيقية هي مجموعة ضخمة تحتوي على جميع الأعداد التي يمكن تصورها، بما في ذلك الأعداد الكسرية والغير كسرية، والأعداد الموجبة والسالبة، والصفر. هناك بعض الأعداد التي لا تنتمي إلى مجموعة الأعداد الحقيقية، مثل:

• الأعداد غير المحددة، مثل √-1.
• ثم الأعداد اللانهائية، مثل ∞.
• ثم الأعداد غير المنطقية، مثل π.

هل كل عدد صحيح هو عدد طبيعي؟

لا، ليس كل عدد صحيح هو عدد طبيعي. العدد الصحيح هو أي عدد لا يحتوي على أجزاء كسريّة، وهو ذاته العدد الذي لا توجد فيه خانات يمين الفاصلة العشريّة، وقد يكون العدد الصحيح موجباً، أو سالباً، أو صفراً.

العدد الطبيعي هو أي عدد صحيح موجب، مثل 1، 2، 3، 4، … لذلك، فإن كل عدد طبيعي هو عدد صحيح، ولكن ليس كل عدد صحيح هو عدد طبيعي.

على سبيل المثال، العدد 0 هو عدد صحيح، ولكنه ليس عددًا طبيعيًا. والعدد -1 هو عدد صحيح، ولكنه ليس عددًا طبيعيًا. والعدد 15 هو عدد طبيعي، وبالتالي هو عدد صحيح. وهكذا، فإن مجموعة الأعداد الصحيحة تشمل مجموعة الأعداد الطبيعية، ولكن مجموعة الأعداد الطبيعية لا تشمل مجموعة الأعداد الصحيحة.

أصغر عدد طبيعي

يعتمد ذلك على تعريف الأعداد الطبيعية التي يتم استخدامه. إذا تم تعريف الأعداد الطبيعية بأنها الأعداد الصحيحة الموجبة، فإن أصغر عدد طبيعي هو 1. ثم أما إذا تم تعريف الأعداد الطبيعية بأنها الأعداد الصحيحة الموجبة والصفر، فإن أصغر عدد طبيعي هو 0.

في الرياضيات الحديثة في الاعداد الصحيحة الطبيعية، يُعرَّف الأعداد الطبيعية بأنها مجموعة غير منتهية من الأعداد التي تبدأ بـ 1، ويتم إنشاؤها بواسطة علاقة الترجع: كل عدد طبيعي له موال وهو أيضا عدد صحيح طبيعي، 1 عدد صحيح طبيعي. وبالتالي، إذا تم استخدام هذا التعريف، فإن أصغر عدد طبيعي هو 1. وبناءً على ذلك، فإن الإجابة على سؤال “أصغر عدد طبيعي” هي:

• 1، إذا تم تعريف الأعداد الطبيعية بأنها الأعداد الصحيحة الموجبة.
• 0، إذا تم تعريف الأعداد الطبيعية بأنها الأعداد الصحيحة الموجبة والصفر.
• 1، إذا تم استخدام تعريف الأعداد الطبيعية الحديثة.

هل الصفر من الأعداد الطبيعية؟

نعم، الصفر هو عدد طبيعي. حيث تعرَّف الأعداد الطبيعية بأنها مجموعة الأعداد التي تبدأ من 1 وتستمر إلى ما لا نهاية. يُعرَّف الصفر على أنه عدد طبيعي في العديد من تعريفات الأعداد الطبيعية، بما في ذلك التعريفات الرسمية التي تستخدمها مجموعات الرياضيات.

يمكن أيضًا استنتاج أن الصفر عدد طبيعي من خواص الأعداد الطبيعية. على سبيل المثال، الصفر هو عدد أولي، مما يعني أنه لا يقبل سوى العوامل 1 ونفسه. كما أنه عدد فردي، مما يعني أنه ليس عددًا زوجيًا. هذه هي نفس الخواص التي تميز الأعداد الطبيعية الأخرى.

ومع ذلك، هناك بعض التعريفات للأعداد الطبيعية التي لا تشمل الصفر. هذه التعريفات تُعرف باسم الأعداد الطبيعية غير الصفرية. يستخدم هذا التعريف غالبًا في سياقات حيث يكون الصفر مهمًا، مثل نظرية الأعداد أو المنطق.

بشكل عام، يعتبر الصفر عددًا طبيعيًا في معظم سياقات الرياضيات. ومع ذلك، من المهم أن تكون على دراية بتعريف الاعداد الصحيحة الطبيعية المستخدم في أي سياق معين.

العدد الكسري الصف الرابع

ضمن الحديث عن الاعداد الحقيقية فيما يلي بعض الأمثلة على الأسئلة التي قد يُطلب من الطلاب الإجابة عليها في الصف الرابع حول الأعداد الكسرية:

1. ما هو الكسر الذي يمثل قطعة واحدة من ثلاث قطع؟
2. ثم كيف تكتب الكسر 0.5 ككسر عشري؟
3. ثم ما هو الكسر المختلط الذي يمثل قطعتين وجزء واحد من ثلاث قطع؟
4. ما هو الناتج من جمع الكسرين 1/2 و 1/3؟
5. ثم ما هو الناتج من طرح الكسرين 3/4 و 1/2؟
6. ثم ما هو الناتج من ضرب الكسرين 1/2 و 3/4؟
7. ما هو الناتج من قسمة الكسر 1/2 على الكسر 1/3؟

القسمة للأعداد العشرية

يتم قسمة الأعداد العشرية بنفس طريقة قسمة الأعداد الصحيحة، مع مراعاة وضع الفاصلة العشرية في الناتج في نفس المكان الذي توجد فيه في الأعداد المُقسومة.

تطبيقات الأعداد العشرية

يستخدم الطلاب الأعداد العشرية في العديد من التطبيقات العملية، مثل:

1. قياس الكميات، مثل الطول والوزن والحجم.
2. ثم حساب المبالغ المالية.
3. ثم قياس درجات الحرارة.

ما هو العدد العشري؟

العدد العشري هو عدد يتكون من جزء صحيح وجزء عشري. الجزء الصحيح هو الرقم الموجود على اليسار من الفاصلة العشرية، بينما الجزء العشري هو الرقم الموجود على اليمين من الفاصلة العشرية.

كيف يمكن تمثيل الأعداد العشرية؟

يمكن تمثيل الأعداد العشرية بعدة طرق، منها:

• الكتابة اللفظية: يتم قراءة الجزء الصحيح كما هو، بينما يتم قراءة الجزء العشري على أنه “جزء من عشر”.
• الكتابة التحليلية: يتم كتابة الجزء الصحيح على شكل عدد صحيح، بينما يتم كتابة الجزء العشري على شكل كسر عشري.
• التمثيل على خط الأعداد: يتم رسم خط الأعداد، ثم يتم وضع الجزء الصحيح على الخط، ثم يتم وضع الجزء العشري على مسافة 1/10 من الجزء الصحيح.

ما هي عمليات الأعداد العشرية؟

يتعلم الطلاب في الصف الرابع عمليات الجمع والطرح والضرب والقسمة للأعداد العشرية.

كيف يتم جمع الأعداد العشرية؟

يتم جمع الأعداد العشرية بنفس طريقة جمع الأعداد الصحيحة، مع مراعاة وضع الفاصلة العشرية في الناتج في نفس المكان الذي توجد فيه في الأعداد المضافة.

كيفية يتم طرح الأعداد العشرية؟

يتم طرح الأعداد العشرية بنفس طريقة طرح الأعداد الصحيحة، مع مراعاة وضع الفاصلة العشرية في الناتج في نفس المكان الذي توجد فيه في الأعداد المُطرحة.

كيف يتم ضرب الأعداد العشرية؟

يتم ضرب الأعداد العشرية بنفس طريقة ضرب الأعداد الصحيحة، مع مراعاة وضع الفاصلة العشرية في الناتج في نفس المكان الذي توجد فيه في الأعداد المُضروبَة.

كيف يتم قسمة الأعداد العشرية؟

يتم قسمة الأعداد العشرية بنفس طريقة قسمة الأعداد الصحيحة، مع مراعاة وضع الفاصلة العشرية في الناتج في نفس المكان الذي توجد فيه في الأعداد المُقسومة.

انواع الأعداد الحقيقية

الأعداد الحقيقية هي مجموعة من الأعداد التي تشمل جميع الأعداد التي يمكن التعبير عنها باستخدام الأرقام الطبيعية والصفر والكسرات والأرقام غير النسبية. يمكن تمثيل مجموعة الأعداد الحقيقية على خط الأعداد، حيث تقع الأعداد الموجبة على يمين الصفر، والأعداد السالبة على يسار الصفر. ويمكن تقسيم الأعداد الحقيقية إلى عدة أنواع، منها:

1. الأعداد الصحيحة: هي الأعداد الموجبة والسالبة مع الصفر.
2. الأعداد النسبية: هي الأعداد التي يمكن التعبير عنها ككسر، مثل 1/2 أو 3/4.
3. ثم الأعداد غير النسبية: هي الأعداد التي لا يمكن التعبير عنها ككسر، مثل √2 أو π.

انواع الأعداد الحقيقية للصف الثاني الاعدادي

فيما يلي شرح موجز لكل نوع من أنواع الأعداد الحقيقية:

الأعداد الصحيحة

إن الأعداد الصحيحة هي الأعداد التي يمكن التعبير عنها بدون كسر، سواء كانت موجبة أو سالبة أو تساوي صفرًا. الأعداد الصحيحة الموجبة هي الأعداد التي أكبر من صفر، مثل 1 و 2 و 3. الأعداد الصحيحة السالبة هي الأعداد التي أقل من صفر، مثل -1 و -2 و -3. والصفر هو العدد الصحيح الوحيد الذي يساوي صفرًا.

ما هي الاعداد النسبية؟

الأعداد النسبية هي الأعداد التي يمكن التعبير عنها ككسر، مثل 1/2 أو 3/4. الكسور هي أرقام يمكن كتابتها على شكل كسر، حيث يكون البسط هو الرقم الموجود فوق الكسر، والنصيب هو الرقم الموجود أسفل الكسر.

الأعداد غير النسبية

إن الأعداد غير النسبية هي الأعداد التي لا يمكن التعبير عنها ككسر، مثل √2 أو π. الأعداد غير النسبية هي أعداد حقيقية لا يمكن كتابتها على شكل كسر.

يمكن استخدام الأعداد الحقيقية لتمثيل مجموعة متنوعة من الأشياء، مثل المسافات والكميات والنسب. على سبيل المثال، يمكن استخدام الأعداد الحقيقية لتمثيل المسافة بين نقطتين على خط أو الكمية الموجودة في حاوية أو النسبة بين حجمين. وفيما يلي بعض الأمثلة على الأعداد الحقيقية:

• الأعداد الصحيحة: 1، 2، 3، -1، -2، -3، 0
• الأعداد النسبية: 1/2، 3/4، 5/6، -1/2، -3/4، -5/6
• ثم الأعداد غير النسبية: √2، π، e، √3، √5

قد يهمك

• أمثلة على الأعداد الحقيقية والغير حقيقية
• الاعداد الصحيحة الطبيعية والنسبية
• الاعداد العشرية قراءة وكتابة
• ما هي الاعداد الكسرية للصف الرابع
• جدول الضرب 3 كامل للاطفال