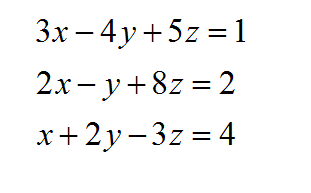
جدول المحتويات
مقدمة
كمهندس أو طالب رياضيات، ربما تكون تعتبر المعادلات الخطية من أبسط المفاهيم التي تتعلمها. ولكن هل تتساءل عن أهمية هذه المعادلات؟ وما الفائدة التي يمكن أن تقدمها لك في الرياضيات والحياة العملية؟ في هذا المقال، سنلقي نظرة على أنواع المعادلات الخطية وأهميتها.
أهمية المعادلات الخطية في الرياضيات والحياة العملية
تعتبر المعادلات الخطية واحدة من العناصر الأساسية في الرياضيات ولها تطبيقات واسعة في الحياة العملية. هنا بعض الأسباب التي تبرز أهمية المعادلات الخطية:
1.التمثيل الرمزي للعلاقات: تساعد المعادلات الخطية في تمثيل العلاقات الرياضية بشكل رمزي ومنظم. فهي تساعد في فهم وتحليل هذه العلاقات بطريقة منظمة ومنطقية.
2.حل المشاكل الحقيقية: تمتلك المعادلات الخطية القدرة على حل مجموعة واسعة من المشاكل الحقيقية في العلوم والهندسة والاقتصاد والإحصاء والعديد من المجالات الأخرى. فهي توفر أداة قوية للتحليل والتحقق واتخاذ القرار.
3.تطوير المهارات الحسابية: يساهم تعلم وحل المعادلات الخطية في تطوير المهارات الحسابية الأساسية مثل الجمع والطرح والضرب والقسمة. فهذه المهارات أساسية في الحياة اليومية وفي مجالات العمل المختلفة.
4.إيجاد العلاقات الترابطية: المعادلات الخطية توفر وسيلة لاكتشاف العلاقات الترابطية بين مجموعة متنوعة من المتغيرات. وهذا يوفر رؤية أعمق في العلاقات الرياضية ويمكن استخدامها في النمذجة والتنبؤ.
لذلك، فإن فهم واستخدام المعادلات الخطية يعتبر أساسيًا في الرياضيات ومفيدًا في الحياة العملية. قم بممارسة حل المسائل وتطبيق هذه المفاهيم في المجالات المختلفة لتعزيز مهاراتك وتحقيق نتائج إيجابية.
المعادلة الخطية بمتغير واحد
إذا كنت تريد تعلم المزيد عن المعادلات الخطية بمتغير واحد، فأنت في المكان المناسب!
1. تعريف المعادلة الخطية بمتغير واحد
المعادلة الخطية بمتغير واحد هي معادلة رياضية تحتوي على متغير واحد فقط وتشمل عمليات الجمع والطرح والضرب والقسمة على نفس الجانبين. على سبيل المثال، المعادلة التالية هي مثال على معادلة خطية بمتغير واحد:
3x + 2 = 8
2. أمثلة وتطبيقات للمعادلة الخطية بمتغير واحد
توجد العديد من التطبيقات العملية للمعادلات الخطية بمتغير واحد في الحياة اليومية وفي مختلف المجالات. على سبيل المثال:
- حساب المسافة المقطوعة باستخدام سرعة ثابتة.
- حساب الإيرادات أو النفقات في العمل.
- حل المسائل الرياضية في مجالات مثل الفيزياء والاقتصاد.
3. طرق حل المعادلة الخطية بمتغير واحد
هناك عدة طرق لحل المعادلة الخطية بمتغير واحد. من بين هذه الطرق:
- استخدام الخوارزمية العادية التي تشمل أعمال الجمع والطرح والضرب والقسمة لتحويل المعادلة إلى شكل تسهل حساباتها.
- استخدام خوارزميات حسابية مثل طريقة نيوتن رافسون للحصول على قيمة تقريبية للحل.
- استخدام الحساب الرمزي أو الحساب الرقمي لحل المعادلات الخطية بمتغير واحد.
في النهاية، يمكن استخدام هذه الطرق لحل المعادلات الخطية بمتغير واحد في العديد من المجالات والتطبيقات المختلفة.
المعادلة الخطية بمتغيرين
في عالم الرياضيات، تعتبر المعادلة الخطية بمتغيرين من أبسط وأساسيّة المعادلات التي يتم دراستها. تحتوي هذه المعادلة على متغيرين ومعاملات خطية، وتتكون من مصفوفة من المتغيرات والثوابت المحددة.
1. تعريف المعادلة الخطية بمتغيرين
المعادلة الخطية بمتغيرين هي معادلة رياضية تتكون من مجموعة من المتغيرات (الأحرف التي ترمز للمجهول) والثوابت المحددة (الأرقام المعروفة)، وتتضمن معاملات خطية. على سبيل المثال، يمكن تمثيل المعادلة الخطية بمتغيرين بالشكل التالي:
a₁x₁ + a₂x₂ + ... + aᵢxᵢ = bحيث x₁, x₂, ..., xᵢ هي المتغيرات، a₁, a₂, ..., aᵢ هي المعاملات، و b هي الثابتة المحددة.
2. أمثلة وتطبيقات للمعادلة الخطية بمتغيرين
تظهر المعادلة الخطية بمتغيرين في العديد من المجالات والتطبيقات، بما في ذلك الهندسة والفيزياء وعلوم الحاسوب والاقتصاد. على سبيل المثال، يمكن استخدام المعادلات الخطية بمتغيرين لحل المسائل المتعلقة بتوازن الميزانية، تصميم الدوائر الكهربائية، وحساب الحركة الخطية للأجسام.
3. طرق حل المعادلة الخطية بمتغيرين
هناك العديد من الطرق المختلفة لحل المعادلات الخطية بمتغيرين، بما في ذلك طريقة التحليل المباشر وطريقة الاستبعاد وطريقة الاستبدال. يعتمد الاختيار بين هذه الطرق على الظروف والاحتياجات الفردية لكل مسألة.
مهما كانت الأساليب المستخدمة، فإن حل المعادلة الخطية يتطلب التعامل مع المتغيرات والمعاملات بشكل صحيح وتطبيق القوانين الرياضية المناسبة.
باستخدام معادلات خطية بمتغيرين، يمكن للمهندسين والعلماء حل العديد من المسائل في مختلف المجالات واتخاذ قرارات مبنية على الحقائق الرياضية.
المعادلة الخطية بثلاثة متغيرات
1. تعريف المعادلة الخطية بثلاثة متغيرات
المعادلة الخطية بثلاثة متغيرات هي معادلة رياضية تحتوي على ثلاثة متغيرات وتتكون من مصفوفة من الأعداد والمتغيرات والعمليات الرياضية البسيطة. عند حل هذه المعادلات، يتم البحث عن القيم التي تجعل المعادلة صحيحة. يتم تمثيل المعادلة الخطية بثلاثة متغيرات في الفضاء الثلاثي البعد بواسطة سطح، والذي يمثل مجموعة الحلول الممكنة.
2. أمثلة وتطبيقات للمعادلة الخطية بثلاثة متغيرات
تستخدم المعادلات الخطية بثلاثة متغيرات في العديد من المجالات المختلفة مثل الهندسة، الاقتصاد، الفيزياء، وعلم الحاسوب. فمن المثاليات الشهيرة لهذا النوع من المعادلات هي الخطوط المستوية والمستعرضات المكافئة في الهندسة الرياضية. يتم استخدام المعادلات الخطية بثلاثة متغيرات أيضًا في التطبيقات الاقتصادية لنمذجة التفاعلات بين المداخل والمخرجات في الأسواق المختلفة.
3. طرق حل المعادلة الخطية بثلاثة متغيرات
هناك طرق عديدة لحل المعادلة الخطية بثلاثة متغيرات، بما في ذلك استخدام طرق التحليل الرياضي والبحث عن القيم المجهولة التي تجعل المعادلة صحيحة. يمكن استخدام أساليب مثل التبادل، الإلغاء، والتعويض لحل هذه المعادلات. كما يمكن استخدام الحسابات المتجهية والتقنيات الجبرية المتقدمة لتبسيط وحل المعادلة الخطية بثلاثة متغيرات.
خلاصة واستنتاجات
بعد هذه المقالة المختصرة حول أنواع المعادلات الخطية، يمكن التوصل إلى عدة استنتاجات حول أهمية هذا المفهوم في الحياة العملية.
أولاً، المعادلات الخطية تعد أساسية في مجمل المجالات الهندسية والعلمية. فهي تسهم في حل المسائل التي تنطوي على علاقات خطية بين المتغيرات. تعتبر مهارة حل المعادلات الخطية أداة أساسية للمهندسين، العلماء والمهن المتعددة التي تعتمد على الرياضيات.
ثانيًا، فهم أنواع المعادلات الخطية يمكن أيضًا أن يساعد في تحسين الإدارة واتخاذ القرارات في الحياة اليومية. بفكرة أساسية، المعادلات الخطية تمثل توازناً بين المتغيرات المختلفة. وباستخدام الرياضيات، يمكن حساب قيم هذه المتغيرات وتوصل إلى حلول مثلى في الوضعيات الحسابية والاقتصادية.
ثالثًا، فهم المعادلات الخطية يمكن أن يكون مفيدًا أيضًا في الحياة الشخصية. يمكن استخدام المعادلات الخطية في تحليل نمط الحياة وتوازن النفس والعلاقات الشخصية. يمكن للمفاهيم الرياضية المبنية على المعادلات الخطية أن تمنحنا فهمًا أعمق للعالم من حولنا ومساعدتنا في اتخاذ القرارات.
باختصار، فإن فهم أنواع المعادلات الخطية واستخدامها يمكن أن يكون مفيدًا في الحياة العملية والإدارة والحياة الشخصية. يمكننا استخدام هذه الأداة الرياضية للتحسين والتفكير الإبداعي في مجموعة متنوعة من المجالات.